 (2.1-1)
(2.1-1)This chapter discusses the role of reliability analysis in the design process of drive systems at the Mechanical Engineering Department of the Construction Division of the Ministry of Transport, Public Works, and Water Management. It describes the design process of drive trains of civil structures, various reliability analysis techniques, and the functions of a drive system. These are steps used to find an automated reliability analysis method, which is also described and demonstrated in this chapter.
This section describes the design process for drive trains of infrastructural works, such as moveable bridges, lock gates, and storm surge barriers. First, the total realisation process, of which the design process is a part, is outlined. Then, the role of reliability analysis in the design process is discussed.
The realisation of infrastructural works is a complex process. To reduce the complexity, the project manager decomposes this job into phases. A phase is a bundle of tasks, that can be controlled in complexity, time, and costs. The Construction Division usually separates the realisation of infrastructural works into the phases:
In the initiation phase the principal and a project manager of the Construction Division define the project goal. The project manager then composes a project plan. This plan describes the project goal, approach, project risks (FMEA), activities in all project phases, use of personnel, costs, quality, information flow during the project, and project organisation. The principal accepts the plan, if he agrees with it.
In the conceptual design phase the project team creates a number of design solutions. A designer determines the main dimensions of each solution. Examples: diameter and length of shafts, ratio of the gearbox, and the power of the engine. He validates these dimensions with a static analysis, and optimises each solution to reduce the costs. The result of this phase is a rough drawing, a rough static analysis report, and a rough cost estimate for each solution. The project team evaluates the solutions and recommends to the principal which one is the most optimal solution. The principal chooses one solution for further detailing in the design phase.
In the design phase the chosen variant is developed further. A designer determines the dimensions of the details of the chosen solution. He validates these dimensions with a static analysis, and optimises the structure to reduce the costs. For some structures, a risk analysis expert executes a fault tree analysis, after the designer has determined all the details. The result of this phase is a detailed (set of) drawings, a detailed static analysis report, an accurate cost estimate, and sometimes a fault tree analysis report.
In the specification phase the project team finishes the detailing of the design, prepares the contract, and sends out requests for proposal to different contractors. The request contains both drawings and specifications in text.
In the (beginning of the) construction phase a contractor is chosen. During the construction phase, the contractor works on further detailing of the design, and builds the infrastructural work. The contractor submits the detailed drawings and calculations for the approval of the project team. At the end of this phase, the contractor delivers the structure to the project manager, and the project manager delivers the structure to the principal.
In the after care phase the project team composes a maintenance plan. This plan advises the principal about maintenance and replacement intervals of components, and a conservation schedule for steel parts.
As demonstrated above, designing takes place in various phases. It takes place in the conceptual design phase, the design phase, the specification phase, and the construction phase. However, the major design decisions are made in the first two phases: the conceptual design phase, and the design phase. Figure 2.1-1 describes the design process in these two phases.

The reliability analysis takes place at the end of the design process, after the layout of the structure is determined. The role of the analysis is to verify if the reliability of the structure satisfies the demanded reliability.
However, at the end of the design process, it to costly, or there is not enough time available to introduce major changes in the structure. Therefore, the results of the analysis have little influence on the design.
The reliability analysis would have a major influence on the design, if it were to be applied during the conceptual design. This would result in more reliable and less expensive structures; a structure that is reliable in concept is less expensive than a structure that is not reliable in concept, but that was improved in a later phase of the design process.

It is known that about eighty percent of the costs of a design are determined in the first twenty percent of the time. This means that eighty percent of the costs are determined in the conceptual design phase. Therefore, the price of a concept is a major issue in pre-design. However, the most affordable design usually is not the safest solution. Therefore, a designer should not make his decisions based on costs alone. Not only should a designer produce a cost-effective design, he should also make a reliable design. Reliability analysis gives a designer the possibility to make decisions based on more aspects than costs only, since it gives him the opportunity to optimise the reliability and costs.
In conceptual design, the role of reliability analysis is to optimise the costs and the reliability. In Figure 2.1-2, the optimisation is placed in the main iteration loop of the conceptual design process.
Beem [19] writes about the optimisation between the costs and the reliability: ‘A major issue for the selection of solutions is the price-performance ratio. Besides the building costs, the price of the design solutions is composed of all the costs during the life cycle of a structure, which are necessary to fulfil its functional demands.’ ‘The life cycle costs, CL, are composed of three parts: investment costs, Ci, the present value of the operational costs, Co (operators, energy), and the present value of the inspection, maintenance, and replacement costs, Ci,m,r.’
 (2.1-1)
(2.1-1)
In this equation r is the annual interest, i is the annual inflation, and g is the annual growth. An usual value for r - i - g is 0.05.
To compare life cycle costs and reliability, Beem also expresses failure and unavailability in costs. The theory is applied to navigation locks. Equation (2.1-1) is expanded with the expectation value of the costs for waiting ships due to the unavailability of the structure. Causes of unavailability are external circumstances, such as extremely high tide, failure and repair, and maintenance. It is also possible to expand the formula with the expectation values of other costs caused by failure or unavailability, Cf,u, such as costs from flooding. The most optimal solution is the one with the lowest total costs, Ctot.
 (2.1-2)
(2.1-2)Vrijling [42] states that the investment costs, Ci, the inspection, maintenance, and replacement costs, Ci,m,r, and the costs of failure or unavailability, Cf,u, are a function of the probability of failure Pf and the repair time Tr. To reduce the costs of failure, it is necessary to reduce the probability of failure. This reduction can be achieved by improving the structure, or intensifying inspection and maintenance, which increases the investment costs and the maintenance costs. The economically optimal structure is the structure with minimal total costs:
 (2.1-3)
(2.1-3)Figure 2.1-3 is a graphical representation of equation (2.1-2) and shows the optimum, represented by minimal total costs.

The most frequently used reliability analysis techniques are: Failure Modes and Effects Analysis (FMEA), Fault Tree Analysis (FTA), and event tree analysis. Appendix D, Beem and others [8], Henley [11], Rao [12], Knezevic [13], Van Gestel and others [22], O’Connor [44], Carter [45], Zacks [55], Lewis [56], Ushakov [57], Vrijling [60], and Ansell [64] describe these techniques in detail. This section gives an overview of these techniques.
FMEA is a technique to make an inventory of all possible failure modes. A risk analyst applies this technique, when he wants to answer the question: ‘What can go wrong with this structure?’. With a systematic approach he tries to find the complete set of failure modes of the structure. The result of the analysis is a long list of all possible failure modes.
Method: Divide the structure into components. Then, list the failure modes of each component in a table.
Not all modes in this table are of importance. Some of them could merely cause an inconvenience, while others could cause a disaster. To separate the important failure modes from the irrelevant ones, the analyst can list the effect and criticality of each failure mode. This solution of FMEA is known as Failure Modes Effects and Criticality Analysis (FMECA). Table 2.2-1 shows the relationship between effect, probability, and criticality.
|
Effect |
Probability of occurrence |
Criticality |
|
Small | Low | Low |
| Small | High | Low |
| Large | Low | Low |
| Large | High | High |
A designer should take precautions to prevent the occurrence of critical failure modes. Whether or not a failure mode is critical, depends on the effect and on the probability of occurrence. When either the effect of a failure mode is small, or probability of occurrence is low, the criticality is low. However, when both the effect is large, and the probability of occurrence is high, the criticality is high. The risk analyst can express the effect and criticality of a failure mode qualitatively with high or low. He can also express it quantitatively with a 1 for low and a 10 for high. He can then obtain a quantitative value for the criticality by multiplying the effect and the probability: effect probability = criticality. Table 2.2-2 is an example of a table format to use in a FMECA.
| Component | Failure mode | Effect | Probability | Criticality |
|
|
|
|
|
|

Fault Tree Analysis (FTA) is a technique to analyse one single failure mode. A risk analyst applies this technique, when he wants to answer the question: ‘What causes this failure mode?’. The result of the analysis is a set of combinations of failing components, which cause failure of the total structure, along with a quantification of the probability of failure. The results of the analysis also show which combination of components has the highest contribution to the total probability of failure.

Method: Define the failure mode that has to be analysed. This failure mode is called the top event, because it is placed at the top of the fault tree. Examples of top events: ‘the bridge does not open’, ‘the bridge does not close’. First, trace the location or component, where the top event occurs. Failure can occur by failure in the component itself, or by failure in bounding subsystems. Example: an electric wire can fail because it is broken, or because the power supply does not work. Second, place a component or set of components, whose failure results in the top event, in the fault tree. Third, consider all bounding subsystems. Place a subsystem or a set of subsystems in the fault tree, whose failure contributes to the failure of the previous component. Repeat this algorithm for this subsystem. Systematically follow the entire system. Quotation: ‘Follow the copper road.’ [R.W. van Otterloo (KEMA)], which means follow the electrical wires to find the components that must be put in the fault tree. Figure 2.2-1 shows a scheme of a hydraulic system. The fault tree in Figure 2.2-2 describes the failure of the hydraulic system.
A combination of failing components, which causes failure of the total structure, and contains as few components as possible, is called a minimal cut set. The fault tree is reduced with Boolean algebra to find these sets. Figure 2.2-3 shows a reduced fault tree; the minimal cut sets are:

It is necessary to quantify the fault tree to find the probability of failure for the total structure, and which components and minimal cut sets have the highest contribution to this probability of failure. A designer can improve parts of the structure, if he judges that the probability of failure is too high. Chapter 5 demonstrates how to quantify a fault tree. If failure of the components occurs per demand, and if failure of the components is independent, the probability of failure for the minimal cut sets can be calculated by multiplying the probabilities of failure of the components. The probability of failure for the total structure can be calculated by adding the probabilities of failure of the minimal cut sets.
Event tree analysis is a technique that defines all possible states of a structure, including the working state. A risk analyst applies this technique when a structure can partially fail and function (at a reduced level) at the same time. For more about partial mission completion this thesis refers to Bedford [61]. Example: a pumping-engine with two pumps can still produce flow when one of the pumps does not work. However, it does not produce to its full capacity. It fails, but it also works. The risk analyst can not use fault tree analysis in this situation, since fault tree analysis only analyses total failure of a structure. The result of the event tree analysis is a set of all possible states in which a structure can exist, along with the probability of occurrence for each state.
Method: Divide the structure into components. Define failure modes for each component. The occurrence of a failure mode is an event. Define the failure modes along the horizontal axis of a diagram. Then, draw a horizontal binary tree. The tree splits up into a true branch and a false branch at each event. Determine in which state the structure is for all paths through the branches, and calculate the probability of each branch at the end of the tree. Combine the probabilities of the branches that have the same state.
An event tree grows in width exponentially. Therefore, an event tree analysis can only be applied to small sets of components.

This section derives an abstract description of the functions of a drive system. This description is necessary to automate reliability analysis.
Usually a drive system is part of a larger structure. It supports this structure to fulfil one of its functions. This thesis focuses on drive systems in infrastructural works, such as moveable bridges, navigation locks, and storm surge barriers. This section considers the functions of these structures, and how the drive trains contribute to these functions.
The main functions of a moveable bridge are to allow road traffic to pass over water, and ships to pass under the bridge. Besides these main functions the bridge has secondary functions, such as preventing people and vehicles from falling into the water, preventing collisions with ships, and being aesthetically pleasing. Table 2.3-1 shows the contribution of the drive train to these functions.
|
Main functions |
Contribution of drive train |
|
Letting road traffic pass over water. | If the bridge is open, the drive train closes the bridge. |
|
Letting ships pass under the bridge. | The drive train opens the bridge. |
|
Secondary functions |
|
|
Preventing people from falling into the water. | None, barriers prevent people from falling into the water when the
bridge is open (of course the barrier has a drive train also, but that
is not considered here), and rails prevent people from falling into the
water when the bridge is closed. |
|
Preventing vehicles from falling into the water. | None, barriers prevent vehicles from falling into the water when the
bridge is open (of course the barrier has a drive train also, but that
is not considered here). |
|
Preventing collisions with ships. | The drive train opens the bridge. Traffic lights show the captain whether he can pass through. |
|
Being aesthetically pleasing. | None. |
The main functions of a navigation lock are being a water barrier, and letting ships through. The lock has secondary functions, such as a passage for people over the lock doors, preventing people from falling into the water, and preventing collisions with ships. Table 2.3-2 shows the contribution of the drive train to these functions.
|
Main functions |
Contribution of drive train |
|
Being a water barrier. | The drive trains close the doors. |
|
Letting ships through. | The drive trains open and close the lock doors. |
|
Secondary functions |
|
|
Giving passage to people over the lock doors. | The drive trains close the doors. |
|
Preventing people from falling into the water. | None. Rails on the lock doors prevent people from falling into the
water, when they walk over the doors. The shores of the navigation lock
should be clean and clear; there should not be objects that could make
people stumble, and fall into the water. |
|
Preventing collisions with ships. | The drive trains open the doors. Traffic lights show the captain whether he can pass through. |
The main functions of a storm surge barrier are (of course) being a water barrier, letting water in and out, and letting ships through. The lock has secondary functions, such as preventing collisions with ships. Table 2.3-3 shows the contribution of the drive train to these functions.
|
Main functions |
Contribution of drive train |
|
Being a water barrier. | The drive train closes the door. |
|
Letting water in and out. | The drive train opens the door, and holds it in the open position. |
|
Letting ships through. | The drive train opens the door, and holds it in the open position. |
|
Secondary functions |
|
|
Preventing collisions with ships. | The drive train opens the door, and holds it
in the open position. Traffic lights show the captain whether he can pass
through. |
In all of these cases, the drive train supports the structure to fulfil its main functions. The function of the drive train is to move (open, close) or hold some sort of substructure. To move this substructure, the drive train needs to execute a motion and carry a load. An example of a storm surge barrier demonstrates that the functions of a drive train can be decomposed in two functions: carrying load, and executing motion.

|
Function |
Direction of load |
Direction of motion |
|
Keep barrier open | Down | - |
|
Close barrier | Down | Down |
|
Open barrier | Down | Up |
Figure 2.3-1 shows a model of a storm surge barrier. The drive train of the barrier has to keep it open when there is no storm. When there is a storm, the drive train closes the barrier. When the storm is over, the drive train opens the barrier.
Table 2.3-4 demonstrates how to decompose the functions of the drive train of the storm surge barrier into the functions carrying load and executing motion.
Drive systems fulfil many tasks, such as opening a bridge, closing a bridge, moving a lock gate, and holding a lock gate against water pressure. It is possible to decompose the task opening a bridge into the functions executing a motion and carrying load (acceleration, wind). It is also possible to decompose the other examples into these functions. This leads to the assumption, that all functions of a drive system can be decomposed into: 1 carrying load, 2 executing motion.
All functions of a drive system can be decomposed into:
1 carrying load;
2 executing a motion.
It is possible to generalise this assumption: the major function of a drive system is to supply energy. This generalised function can be divided into several specialised sub-functions: Load and displacement (motion) define energy. Pressure and flow also define energy. Thus, the functions of a drive system are supplying pressure, and producing flow. Temperature and heat also define energy. Thus, the functions of a drive system are maintaining a temperature, and producing heat. Voltage and current also define energy. Thus, the functions of a drive system are maintaining a voltage, and producing current. In this thesis we focus on the functions carrying load, and executing motion.
A failure modes and effects analysis (FMEA) is not useful to analyse the reliability concerning these functions. It does not describe the cause of failure for a single function. This type of analysis is useful to find failure for more functions, than the two that are described above.
An event tree may be an useful technique to describe failure of these two functions. However, this technique only produces practical results for small sets of components.
Therefore, a fault tree analysis is the most appropriate technique used to analyse the reliability of a drive train concerning these functions. Not able to execute motion, and not able to carry load are the top events of the fault trees.
It was concluded in the section above, that fault tree analysis is the most appropriate technique to use in the conceptual design phase when analysing the reliability of the functions of a structure. Several researchers have attempted to automate fault tree analysis. This section briefly describes their approach, followed by a discussion of the first attempt [5], and final approach used to automate the fault tree analysis for this research project.
Kócza [28] uses system models, a type of flow diagram, to automate fault tree analysis. The system model consists of blocks, which represent the components of a structure. The blocks are connected with arrows, that represent the signal flows. Kócza’s software automatically translates the system model into a fault tree.
Robitaille [32] and O’Hern [32b] use the Digraph Matrix Analysis technique (DMA) developed by Sacks [33], to automate fault tree analysis. Digraph Matrix Analysis is based on Petri Net analysis, a type of flow diagram analysis. The diagram consists of nodes, that schematically represent the components of a structure. Arrows representing flows determine the flow direction between the nodes. Sacks’ software automatically translates the Digraph into a fault tree.
Matsuoka [34] uses the Go-Flow methodology. The Go-Flow methodology gives a time dependent, probabilistic, and logic representation of a structure. A Go-Flow chart consists of signal generators, logical operators, and probabilistic operators. This methodology replaces the fault tree analysis technique, since it has extra functionality.
Yamashina [35] uses semantic flow diagrams to automate fault tree analysis. The diagram consists of nodes, that schematically represent the components of a structure, and nodes that represent the flows in the structure. Arrows represent the relationships between the nodes. Yamashina’s software automatically translates the flow diagrams into a fault tree.
Similar to Robitaille and O’Hern, Kohda [36] uses Petri Nets to automate fault tree analysis. Kohda also automates event tree analysis using Petri Nets.
Takahashi [37] developed a component modeller to define a structure. The modeller automatically translates the component model into a flow diagram, and it automatically translates the flow diagram into a fault tree. The component model is an extra layer above the flow diagram. This layer gives the designer or risk analyst a more comprehensive representation of the structure.
All of the references above use some type of flow diagram to automate fault tree analysis. The flow diagrams give an abstract representation of the structure. The fault tree generation programs help prevent the risk analyst from making errors. However, they do not yet help the designer. For the designer, these programs change the problem from ‘how to make a fault tree’ to ‘how to make a flow diagram’. Takahashi [37] solved this problem. He adds an extra shell to his software, that hides the flow diagram. This shell uses components such as pumps, and valves to model a structure. Thus, the designer does not need to have knowledge about flow diagrams to execute a fault tree analysis.
However, Takahashis’ components are very schematic. They do not support the designer in defining the geometry of a structure. The next step is to introduce components with real dimensions to support the designer in defining both the geometry of a structure as well as the reliability analysis. This research project attempts to achieve this.
First attempt
The first attempt to automate fault tree analysis for this research project also used a flow diagram approach [5]. A prototype of an automated fault tree analysis program was developed to test the approach. This software contains a component modeller, which uses components such as hydraulic cylinders, pipes, valves, and pumps, and a fault tree generator.
The component modeller stores the model of a structure as components and nodes. The nodes of a component are connection points. If two components have a node in common, they are connected.

Besides the topology of the structure, the nodes also describe the function of the components: the nodes of a pipe should produce a flow, the nodes of a cylinder should produce a flow and cause a displacement. The nodes describe the interface between connected components. Figure 2.4-1 is an example of a pipe component.

Failure of a component can occur by failure in the component itself, or by failure of an adjacent component. Each component has a local fault tree, that describes failure by the failure in the component itself, and failure by the interfaces on the nodes. Figure 2.4-2 is an example of a local fault tree for a pipe component.
To create the global fault tree of a structure the program starts at the node, that describes the main function of the structure. This node is connected to a component. The local fault tree of this component is the base of the global fault tree of the structure. The local fault tree refers to the interfaces with the component nodes. The program links the local fault trees of other components on these positions in the fault tree. A recursive algorithm walks through the total structure in this way. Some structures contain loops, for instance in piping. Figure 2.4-3 demonstrates this with a simple hydraulic scheme. To prevent the algorithm from running in circles in the structure, and entering an algorithmic infinite loop, the program sets flags at each branch of pipes and other components.
Although the algorithm produces valid fault trees for all structures that were tested, it is too complex to prove that it produces valid results in all cases, since the structures often have a network architecture, and the way the algorithm navigates through the structure is not always clear. Therefore, a more robust algorithm was developed. This algorithm is described below.

In section 2.3 the functions of a drive train were decomposed into the functions carrying load and executing motion. The finite element method can be adapted to mathematically describe these functions. The equilibrium equations, that describe the equilibrium of the external loads f on nodal points and the internal element stresses , will be used to represent the function carrying load:
DT. sigma = f (2.4-1)
The continuum equations, that describe the relationships between nodal displacements u and deformations , will be used to represent the function executing motion:
epsilon = D. u (2.4-2)
Each elemental stress represents a failure mode of an element that might fail to fulfil the function carrying load, if it is broken. In this case the finite element equations prescribe an elemental stress to be equal to zero. Each elemental deformation represents a failure mode of an element that might fail to fulfil the function executing motion, if it is blocked. In this case the finite element equations prescribe an elemental deformation equal to zero.
Assume that a certain combination of components has failed. It is possible to express this in the finite element equations above. When it is not possible to find a permissible stress distribution , or kinematically permissible displacement field u, the combination of failing components is a failure mode. Otherwise, it is not. All failure modes are found by trying all combinations. A structure fails, when equation (2.4-1) or (2.4-2) can not be solved for the prescribed loads and displacements. An unsolvable set of equations is the mathematical representation of a failing drive train.
This theory was implemented in an algorithm, that finds the minimal cut sets of a fault tree by simply trying all combinations of failing elemental deformations and stresses. A combination is a failure mode, when the system of equations can not be solved.
The algorithm was implemented into a software package. The design process is as follows: The designer creates design concepts, and defines the functions of the structure. Then, he decomposes these functions into the basic functions carrying load and executing motion. The software helps the designer to build a component model of the design concepts. For each function a separate model is necessary. The software automatically translates the component model into a finite element model, generates the minimal cut sets of the fault tree, and quantifies the fault tree.
Like Takahashi’s [37] program, the software package of this research project has an extra component shell, that hides the finite elements model from the designer. This shell uses components, such as pumps and valves, to model a structure. Thus, the designer does not need to have knowledge about finite element theory to execute a fault tree analysis. Figure 2.4-4 shows which part of the modelling and analysis process is supported by the software package.

This section demonstrates how to optimise a drive train with the software, that was developed in this project. Four different types of drive trains for the storm surge barrier of Figure 2.5-1 are evaluated. Table 2.3-4 shows that five analyses per solution are necessary. The function keep barrier open is translated into a model with a downward load on the gate. The brake in the drive train carries this load. The functions open barrier and close barrier are each translated to two models per function. One model with a downward load on the gate. The engine of the drive train carries this load. In the second model, the gate has a prescribed motion downward or upward.



The first type of the drive train contains a single engine, a coupling, a single brake, a coupling and a gearbox.


The second type of drive train contains double engines, couplings and brakes.


The third type of drive train contains double engines, an extra gearbox and two extra couplings.

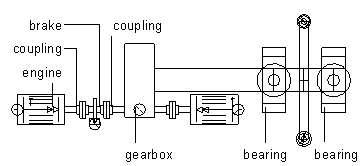
The fourth type of drive train contains double engines, one extra coupling and no extra gearbox.
The paragraphs below show a part of the output for the analysis of Type II for the function carry load while the barrier is being closed:
Analysis of start action period.
The probability of failure is the probability, that a structure has failed in
one cycle of periods (rest, start, action, or stop). The periods, that were
taken into account, are mentioned above. The unavailability refers to the total
time of a cycle. This is the sum of the rest and action interval, regardless
if these intervals were analysed.
Rest interval: 7.2e+02 h,
Amount of queries per unit time: 1.4e-03 1/h,
Action interval: 1.0e+00 h.
Probability of failure (independent failure): 3.9e-06
Unavailability (independent failure): 2.6e-07
Probability of failure (dependent failure, beta: 0.1): 2.9e-05
Unavailability (dependent failure, beta: 0.1): 1.1e-06
5 %, 50 %, and 95 % certainty intervals.
Probability of failure (independent failure): 3.2e-06 3.8e-06 4.3e-06
Unavailability (independent failure): 9.4e-08 2.2e-07 4.9e-07
Probability of failure (dependent failure, beta: 0.1): 1.6e-05 2.7e-05 4.4e-05
Unavailability (dependent failure, beta: 0.1): 3.8e-07 9.1e-07 2.0e-06
Minimal cut set:
Probability of failure (independent failure): 5.1e-08
Unavailability (independent failure): 1.7e-09
Probability of failure (dependent failure): 2.5e-05
Unavailability (dependent failure): 8.3e-07
5 %, 50 %, and 95 % certainty intervals.
Probability of failure (independent failure): 1.4e-08 4.0e-08 9.4e-08
Unavailability (independent failure): 4.3e-10 9.4e-10 3.5e-09
Probability of failure (dependent failure, beta: 0.1): 1.2e-05 2.3e-05 4.0e-05
Unavailability (dependent failure, beta: 0.1): 1.7e-07 6.2e-07 1.7e-06
cname rotgen cmpnr 1 ename beam elmnr 1 defnr 2
Failure mode: Torque engine to low.
Lrest 7.5e-06 Qstart 1.5e-04 Laction 7.5e-05 Qstop 1.5e-05 Trepair 2.4e+01
srest 3.7e-06 sstart 7.5e-05 saction 3.8e-05 sstop 7.5e-06 srepair 1.2e+01
cname rotgen cmpnr 10 ename beam elmnr 10 defnr 2
Failure mode: Torque engine to low.
Lrest 7.5e-06 Qstart 1.5e-04 Laction 7.5e-05 Qstop 1.5e-05 Trepair 2.4e+01
srest 3.7e-06 sstart 7.5e-05 saction 3.8e-05 sstop 7.5e-06 srepair 1.2e+01
Minimal cut set:
Probability of failure (independent failure): 3.9e-06
Unavailability (independent failure): 2.6e-07
Probability of failure (dependent failure): 3.9e-06
Unavailability (dependent failure): 2.6e-07
5 %, 50 %, and 95 % certainty intervals.
Probability of failure (independent failure): 3.2e-06 3.8e-06 4.5e-06
Unavailability (independent failure): 9.2e-08 2.2e-07 4.9e-07
Probability of failure (dependent failure, beta: 0.1): 3.2e-06 3.8e-06 4.5e-06
Unavailability (dependent failure, beta: 0.1): 9.2e-08 2.2e-07 4.9e-07
cname gearbox2 cmpnr 13 ename gear2 elmnr 62 defnr 1
Failure mode: Collapse of gears due to torsional moment ingoing shaft.
Lrest 2.0e-09 Qstart 3.9e-06 Laction 2.0e-09 Qstop 3.9e-07 Trepair 4.8e+01
srest 1.0e-09 sstart 3.9e-07 saction 1.0e-09 sstop 3.9e-08 srepair 2.4e+01
The output on the reliability analysis software contains the following data:
Table 2.5-1 to 2.5-4 show the results of the analyses. The results in Table 2.5-1 and 3 take into account, that failure of the components in a minimal cut set is (partly) dependent. The results in Table 2.5-2 and 4 take into account, that the failure of components is totally independent. The differences between the two calculation methods are a factor 10.
| Type | function | P carry load | highest contrib. | P exec. motion | highest contrib. | P total |
| I | hold | 1.0*10-3 | brake | - | - | 1.0*10-3 |
| I | close | 2.3*10-4 | engine | 3.5*10-4 | brake | 5.8*10-4 |
| I | open | 2.3*10-4 | engine | 3.5*10-4 | brake | 5.8*10-4 |
| II | hold | 1.2*10-4 | brake | - | - | 1.2*10-4 |
| II | close | 2.9*10-5 | engine | 6.7*10-4 | brake | 7.0*10-4 |
| II | open | 2.9*10-5 | engine | 6.7*10-4 | brake | 7.0*10-4 |
| III | hold | 1.0*10-3 | brake | - | - | 1.0*10-3 |
| III | close | 4.5*10-5 | engine | 3.8*10-4 | brake | 4.3*10-4 |
| III | open | 4.5*10-5 | engine | 3.8*10-4 | brake | 4.3*10-4 |
| IV | hold | 1.0*10-3 | brake | - | - | 1.0*10-3 |
| IV | close | 3.0*10-5 | engine | 3.7*10-4 | brake | 4.0*10-4 |
| IV | open | 3.0*10-5 | engine | 3.7*10-4 | brake | 4.0*10-4 |
| solution | function | P carry load | highest contrib. | P exec. motion | highest contrib. | P total |
| I | hold | 1.0*10-3 | brake | - | - | 1.0*10-3 |
| I | close | 2.3*10-4 | engine | 3.5*10-4 | brake | 5.8*10-4 |
| I | open | 2.3*10-4 | engine | 3.5*10-4 | brake | 5.8*10-4 |
| II | hold | 4.3*10-6 | brake | - | - | 4.3*10-6 |
| II | close | 3.9*10-6 | engine | 6.7*10-4 | brake | 6.7*10-4 |
| II | open | 3.9*10-6 | engine | 6.7*10-4 | brake | 6.7*10-4 |
| III | hold | 1.0*10-3 | brake | - | - | 1.0*10-3 |
| III | close | 2.0*10-5 | engine | 3.8*10-4 | brake | 4.0*10-4 |
| III | open | 2.0*10-5 | engine | 3.8*10-4 | brake | 4.0*10-4 |
| IV | hold | 1.0*10-3 | brake | - | - | 1.0*10-3 |
| IV | close | 5.0*10-6 | engine | 3.7*10-4 | brake | 3.8*10-4 |
| IV | open | 5.0*10-6 | engine | 3.7*10-4 | brake | 3.8*10-4 |
| solution | function | U carry load | highest contrib. | U exec. motion | highest contrib. | U total |
| I | hold | 8.0*10-4 | brake | - | - | 8.0*10-4 |
| I | close | 7.5*10-6 | engine | 8.6*10-6 | brake | 1.6*10-5 |
| I | open | 7.5*10-6 | engine | 8.6*10-6 | brake | 1.6*10-5 |
| II | hold | 7.5*10-5 | brake | - | - | 7.5*10-5 |
| II | close | 1.1*10-6 | engine | 1.6*10-5 | brake | 1.7*10-5 |
| II | open | 1.1*10-6 | engine | 1.6*10-5 | brake | 1.7*10-5 |
| III | hold | 8.0*10-4 | brake | - | - | 8.0*10-4 |
| III | close | 2.8*10-6 | engine | 1.0*10-5 | brake | 1.3*10-5 |
| III | open | 2.8*10-6 | engine | 1.0*10-5 | brake | 1.3*10-5 |
| IV | hold | 8.0*10-4 | brake | - | - | 8.0*10-4 |
| IV | close | 1.2*10-6 | engine | 9.3*10-6 | brake | 1.1*10-5 |
| IV | open | 1.2*10-6 | engine | 9.3*10-6 | brake | 1.1*10-5 |
| solution | function | U carry load | highest contrib. | U exec. motion | highest contrib. | U total |
| I | hold | 8.0*10-4 | brake | - | - | 8.0*10-4 |
| I | close | 7.5*10-6 | engine | 8.6*10-6 | brake | 1.6*10-5 |
| I | open | 7.5*10-6 | engine | 8.6*10-6 | brake | 1.6*10-5 |
| II | hold | 2.7*10-6 | brake | - | - | 2.7*10-6 |
| II | close | 2.6*10-7 | engine | 1.6*10-5 | brake | 1.6*10-5 |
| II | open | 2.6*10-7 | engine | 1.6*10-5 | brake | 1.6*10-5 |
| III | hold | 8.0*10-4 | brake | - | - | 8.0*10-4 |
| III | close | 2.0*10-6 | engine | 1.0*10-5 | brake | 1.2*10-5 |
| III | open | 2.0*10-6 | engine | 1.0*10-5 | brake | 1.2*10-5 |
| IV | hold | 8.0*10-4 | brake | - | - | 8.0*10-4 |
| IV | close | 3.3*10-7 | engine | 9.3*10-6 | brake | 9.6*10-6 |
| IV | open | 3.3*10-7 | engine | 9.3*10-6 | brake | 9.6*10-6 |
Type I is the simplest: there are no redundant components in the drive train. The other types contain double or redundant components to improve the reliability. Type II shows, that improving the reliability of the function hold (keep barrier open) has a negative effect on the other functions. Double brakes improve the reliability of the function hold. However, they have a negative effect on the functions close and open. Types III and IV show, that it is only possible to make minor improvements to the reliability of the functions close and open. The brake has a negative effect on the reliability of these functions. However, it is not possible to remove it from the drive train, because it is necessary for the function hold. Type III and IV show, that removing unnecessary components improves the reliability.
Which type should the designer choose? The analysis results show that a type, that is optimal for one function, is not optimal for another function. In the case of the storm surge barrier, it is sensible to give the highest priority to the function close. Thus, the designer will not select Type II. Type III is more expensive and less reliable than type IV, because it contains extra components. Thus, the designer will not select Type III either. Type IV is slightly more reliable (a factor 1½) than Type I. However, it is also more expensive, since it contains an extra engine, coupling, and a more complex gearbox. It is necessary to study the results of the analysis more closely to be able to choose between Type I and IV. Table 2.5-5 and 6 show the distribution of the probabilities of failure of these types.
|
Type I |
5% boundary |
50% boundary |
95% boundary |
|
P carry load | 1.1*10-4 | 2.0*10-4 | 3.6*10-4 |
|
P exec. motion | 1.6*10-4 | 3.1*10-4 | 6.1*10-4 |
|
Type IV |
5% boundary |
50% boundary |
95% boundary |
|
P carry load | 1.7*10-5 | 2.8*10-5 | 4.6*10-5 |
|
P exec. motion | 1.7*10-4 | 3.3*10-4 | 6.3*10-4 |
The distribution function of the total probability of failure is the sum of the distributions of the probability that the drive train is not able to carry the load, and execute the motion. It is not possible to calculate this function directly from Table 2.5-5 and 6. However, it is possible to conclude that the deviation of the probability of failure for Type IV is smaller than the deviation of the probability of failure for Type I. It is also possible to conclude that the 50% boundary of the probability of failure for Type IV is lower than the 50 % boundary for Type I. This means, that Type IV is indeed more reliable than Type I. However, the advantage in reliability is small.
Whether to choose Type IV over Type I depends on the difference in costs and the demanded probability of failure. If the calculated probability of failure for Type I is much larger than the demanded probability of failure, the extra investment of Type IV is not necessary. However, if Type I is barely safe enough, it depends on the costs. If Type I is not safe enough it is necessary to choose Type IV.
This chapter demonstrates, that it is possible to improve a design by applying reliability analysis. It shows how to quantify failure and unavailability in costs, and how to compare them with investment costs to improve the reliability. A better design is not necessarily a design with a higher reliability, but a design with optimal life cycle and failure costs.
It is possible to automate reliability analysis, and to integrate the automated method into the design process. Fault tree analysis appears to be a suitable technique to analyse the reliability of the functions of a structure, and to compare the reliability of different solutions of a structure.
It is possible to give an abstract description of the most important functions of a drive train. This chapter demonstrates how all major functions of a drive train can be decomposed into the basic functions carrying load, and executing motion. The finite element theory describes these functions. The minimal cut sets of a fault tree can be derived directly from the finite elements model.
The theory was embedded in a software package, that helps a designer create design solutions. The software produces comprehensive results, and helps the designer improve the structure, and choose the most optimal solution.
Home Previous page